在c++中用遞迴玩數獨
Algorithm22 Aug 2017
前幾天看到弟弟的朋友提到自己寫了一個解數獨的程式,想一想這的確是一個很好的練習。大學時期,我的程式能力滿悲劇的,因此前些日子在看一些遞迴的範例,趁此機會好好鍛練一番。這篇文章主要記錄自己整個想法與程式。
標題下得很猛,其實就是用 c++ 跟遞迴來解數獨啦!
數獨是甚麼呢?真的沒聽過的人可以看看wiki上面的介紹。
通常是大家拿來打發時間或是動動腦的一個小遊戲。身為懶人工程師的我,打算來寫一支程式自動幫我填完答案。
暴力解
一開始看到數獨會有甚麼想法呢?好吧,既然每一格只能填1到9的數字,那我就用暴力解跟他拚了!而且電腦不是很擅長這種窮舉的方式嗎?
沒錯!對於起頭來說,這個想法既直覺又簡單。這個方法的實作就是簡單的 DFS。想像你有一棵樹,從 root 出發,假設你有 N 個需要填入答案的空格,那麼這個樹的 depth 就是 N + 1。每一個 node 會有 9 個 child。每當你幫一個空格填了一個數字,就前往下一格還沒有被指定數字的空格,不停遞迴下去直到所有格子都填滿了。最後再來檢查這個填法正不正確。
int sudoku[9][9]; // 假設都已經填入題目的數值
void solve(int current_n, int N, ... )
{
if (current_n == N)
{
// 全部都填完了,檢查正確性
}
// 嘗試在目前這格中填入1-9所有可能,然後前往下一個空格
for (int i = 0; i < 9; i++)
{
sudoku[current_row][current_col] = i;
solve(current_n + 1, N, ...);
}
}
這個方法可以行得通沒錯,不過聰明的大家一定有發現許多缺點。
- 每一個空格不一定都能填入 1-9 吧,有些數字可以先濾掉。這樣做太浪費時間了
- 最後都需要檢查整個數獨的正確性,太浪費時間了
沒錯,在遞迴中一個重要的地方就是盡可能減少需要遞迴的次數,只要發現目前的情況不可能是最終答案就不要再嘗試下去了,趕快換一條路吧。
我的解法
在解這個問題的時候,我開始回想我自己以前是怎麼玩數獨的。就以下圖中的黃色空格為例子,我們會先看藍色的直行,發現這格只可以填入 1, 2, 3, 9。接下來我們看粉紅色的橫排,經過篩選之後我們可以填入 1, 2, 3, 4, 5, 7。最後我們看左上角的 block,剩下沒有出現的數字是 1, 2, 4, 7。綜合上面三個方向的觀察,我們可以發現綠色這格可以填入的數字剩下 1, 2。如此一來,當我們抵達這格的時候,我們的迴圈只需要嘗試 1 和 2 這兩個數字。
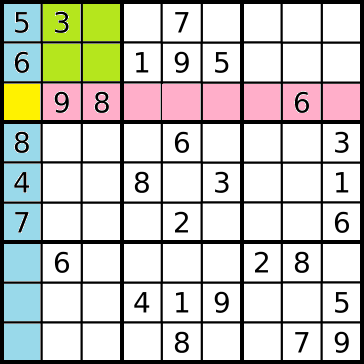
根據上面的寫法,當我們依序填入數字時,尚未有數字的空格所能選擇的數字會越來越少,因為已經被先填入的格子搶先了。當你在 DFS 中碰到一個空格不存在任何可以填入的數字時,代表著前面已經填錯,此路不通,此時就能果斷地放棄這條路。
根據這個簡單的方法,我們可以想出下面這個簡單的遞迴:
- 先為每一行,每一列,每一個區塊都建立一個可填入的數字列表。
- 每當抵達一個空格,利用上面的紀錄來計算出這個空格所能填入的數字列表。
- 依序嘗試各種可能且遞迴下去,如果沒有可填入的直接返回。
- 每當填入一個數字就得更新每一行,每一列,每一個區塊的可填入數字列表。
- 遞迴直到所有表格都填滿了,此時也不用驗證,這就是答案! 因為中途只要有任何錯誤就會直接返回了,所以能完成的一定就是我們要的。
有了基本想法後我們就來寫程式吧。
Global variable
這邊讓我偷懶一下使用 global variable,這不是一個好編程方法,純粹是為了方便。
因為數獨是 9 x 9,我不喜歡直接把一個數字寫進去,所以用一個變數來表示而已。
#define MAX_SIZE 9
這邊我用 matrix來表示我數獨的表格。
為了測試,我先寫死了兩組數獨,一個簡單與一個困難的,後面會看到還能讓使用者輸入。
int matrix[MAX_SIZE][MAX_SIZE] = {
#if USE_HARD_SUDOKU
8,0,0,0,0,0,0,0,0,
0,0,3,6,0,0,0,0,0,
0,7,0,0,9,0,2,0,0,
0,5,0,0,0,7,0,0,0,
0,0,0,0,4,5,7,0,0,
0,0,0,1,0,0,0,3,0,
0,0,1,0,0,0,0,6,8,
0,0,8,5,0,0,0,1,0,
0,9,0,0,0,0,4,0,0
#else
3,9,0,6,0,7,5,1,0,
5,0,8,9,0,2,0,4,3,
7,0,1,0,0,8,0,0,9,
8,1,0,4,6,0,3,9,2,
6,3,0,1,2,9,0,7,4,
0,2,9,0,7,0,6,5,0,
0,5,3,0,0,0,4,8,0,
1,0,4,0,0,6,0,0,7,
0,0,6,0,8,4,0,2,5
#endif
};
在想法中我有提到,我們可以為每一行每一列每一個區塊都保存一份可以填入的數字列表。這樣我們在抵達一個空格時,可以很快的找出在目前的情況下可以填入的數字們。而我使用vector的原因很簡單,因為每當你填妥了一個數字,這些都需要動態更新。
vector<int> row_vec[MAX_SIZE];
vector<int> col_vec[MAX_SIZE];
vector<int> block_vec[MAX_SIZE];
印出現在的數獨結果
這個應該不用說明了吧,還是得顯示一下結果。
void print_matrix()
{
cout << "=====current====" << endl;
for (int i = 0; i < MAX_SIZE; i++)
{
cout << "|";
for (int j = 0; j < MAX_SIZE; j++)
{
cout << matrix[i][j];
if (j % 3 == 2)
cout << "|";
}
cout << endl;
if (i % 3 == 2)
cout << "-------------" << endl;
}
}
計算總共幾個需要填入的空格與座標
為了不要處理走到邊界的問題,同時為了讓遞迴寫起來更順手,我想先紀錄總共有幾個答案需要我來填,然後他們各自的座標。這樣在遞迴的時候我就能直接跳到下一個該關注的座標了!很方便,而且這個只需要掃描一次就好,不花太多時間。
int get_empty_num(vector<int>& row_list, vector<int>& col_list)
{
int num = 0;
row_list.clear();
col_list.clear();
for (int i = 0; i < MAX_SIZE; i++)
{
for (int j = 0; j < MAX_SIZE; j++)
{
if (matrix[i][j] == 0)
{
num++;
row_list.push_back(i);
col_list.push_back(j);
}
}
}
return num;
}
利用座標查詢所在的區塊index
在全域變數中有一個 block_vec,當我們走到一個座標,我們需要知道目前座標位於的這個 block 的 index 是多少,才能去 block_vec 中取出現在能填入的數字們。因此特別用一個 function 吃座標並且回傳現在 block 的 index。
我 index 的數字從左上角以0開始,先向右後向下遞增。
int get_block_num(int row, int column)
{
// 012
// 345
// 678
int r = row / 3;
int c = column / 3;
return r * 3 + c;
}
在開始前先建立好每個row每個column每個block所能填入的數字列
在我們取得謎題之後,我們得先確定這個謎題是正確的,也就是說在同一 row 中不會出現兩個相同的數字,column 與 block 也是相同的原理。接著,我們得先幫每一 row 每一 column 每一 block 建立還沒被填入的數字名單。供接下來的遞迴使用。
這邊以 row 為例子。檢查整個 row 有沒有重複的數字,如果出現的話就回傳 -1 表示這是個不好的 input。與此同時也記錄 1-9 哪些數字還沒出現,最後再將這些還沒出現的數字放入 row_vec[row]中。
經過這個步驟,row_vec 就存放了每一個 row 還沒出現的數字,這些數字在接下來的程式中可以被拿來使用。
column 與 block 則以此類推。
int check_and_generate_info()
{
// row
for (int i = 0; i < MAX_SIZE; i++)
{
bool check[MAX_SIZE] = {false};
for (int j = 0; j < MAX_SIZE; j++)
{
int value = matrix[i][j] - 1;
if (value < 0)
continue;
if (check[value])
return -1;
check[value] = true;
}
for (int j = 0; j < MAX_SIZE; j++)
{
if (!check[j])
row_vec[i].push_back(j + 1);
}
}
// column
for (int j = 0; j < MAX_SIZE; j++)
{
bool check[MAX_SIZE] = {false};
for (int i = 0; i < MAX_SIZE; i++)
{
int value = matrix[i][j] - 1;
if (value < 0)
continue;
if (check[value])
return -1;
check[value] = true;
}
for (int i = 0; i < MAX_SIZE; i++)
{
if (!check[i])
col_vec[j].push_back(i + 1);
}
}
// block
for (int block = 0; block < MAX_SIZE; block++)
{
bool check[MAX_SIZE] = {false};
int row_start = (block / 3) * 3;
int col_start = (block % 3) * 3;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
int value = matrix[i + row_start][j + col_start] - 1;
if (value < 0)
continue;
if (check[value])
return -1;
check[value] = true;
}
}
for (int i = 0; i < MAX_SIZE; i++)
{
if (!check[i])
block_vec[block].push_back(i + 1);
}
}
return 0;
}
為當前的座標尋找可以填入的數字
當我們走到某一個地點時,需要觀察他所在的 row, column, block,然後從中找出一組可以填入的數字。而這個數字需要同時存在 row_vec[row], col_vec[column], block_vec[block] 中。這個 function 就是在做這件事情,找出存在三者交集中的數字。
這個 function 存在許多更好的實踐方法,這邊只是其中一種簡易的方法。
vector<int> find_same_num(vector<int>& row_v,
vector<int>& col_v,
vector<int>& block_v)
{
vector<int> result;
bool r[MAX_SIZE] = {false};
bool c[MAX_SIZE] = {false};
bool b[MAX_SIZE] = {false};
for (int i = 0; i < row_v.size(); i++)
r[row_v[i] - 1] = true;
for (int i = 0; i < col_v.size(); i++)
c[col_v[i] - 1] = true;
for (int i = 0; i < block_v.size(); i++)
b[block_v[i] - 1] = true;
for (int i = 0; i < MAX_SIZE; i++)
{
if (r[i] && c[i] && b[i])
result.push_back(i + 1);
}
return result;
}
重頭戲,遞迴本身
終於來到重點了!先來說說參數
- curr_n : 現在的 index
- total_n : 需要填入答案的空白格總數
- row_list : 帶入 curr_n 可以查詢 row 座標
- col_list : 帶入 curr_n 可以查詢 column 座標
首先我們會先有現在的 row, column, block,藉由他們的 index,我們可以取從 find_same_num 這個 function 取得目前這個空格所可以填入的數字列表。如果很不幸地,這個地方沒有任何數字可以填入,那們代表此路不通,趕緊 return。
如果有的話,我們就依序填入可能的數字,然後前往下一格。這邊得注意,當你填入一個數字,代表你必須將這個數字從可以使用的數字列表中移除,因為他已經被使用了。而當遞迴返迴時,你就可以將這個數字再次放回可以使用的數字列表中,因為此時你要嘗試另外一個數字,原本的數字又可以被某一格使用。這就是那個 for 迴圈在做的事情。
這邊我是用了 find 與 erase,應該有更好的方法來做這件事情。
void runKernel(int curr_n, int total_n,
vector<int>& row_list, vector<int>& col_list)
{
if (curr_n == total_n)
{
print_matrix();
return;
}
int row = row_list[curr_n];
int col = col_list[curr_n];
int block = get_block_num(row, col);
vector<int> candidates = find_same_num(row_vec[row], col_vec[col], block_vec[block]);
if (candidates.size() == 0)
return;
for (int i = 0; i < candidates.size(); i++)
{
int value = candidates[i];
vector<int>::iterator iter;
iter = find(row_vec[row].begin(),
row_vec[row].end(), value);
row_vec[row].erase(iter);
iter = find(col_vec[col].begin(),
col_vec[col].end(), value);
col_vec[col].erase(iter);
iter = find(block_vec[block].begin(),
block_vec[block].end(), value);
block_vec[block].erase(iter);
matrix[row][col] = value;
runKernel(curr_n + 1, total_n, row_list, col_list);
matrix[row][col] = 0;
row_vec[row].push_back(value);
col_vec[col].push_back(value);
block_vec[block].push_back(value);
}
}
用 main 來執行程式吧
主要元素都準備好了,接下來就寫一個 main 來執行吧。
這邊我 define 了一個 DEBUG_MODE。
- 使用 DEBUG_MODE : 會用我寫死的數獨來跑
- 不使用 DEBUG_MODE : 請使用者輸入數獨題目
int main()
{
#if !DEBUG_MODE
cout << "Please enter the numbers : " << endl;
for (int i = 0; i < MAX_SIZE; i++)
{
char in[10];
cin >> in;
if (strlen(in) != MAX_SIZE)
{
cout << "Error input!!!" << endl;
return 0;
}
for (int j = 0; j < MAX_SIZE; j++)
{
int value = in[j] - '0';
if (value > 0 && value < 9)
matrix[i][j] = value;
else
matrix[i][j] = 0; // unknown
}
}
#endif
print_matrix();
if (check_and_generate_info() < 0)
{
cout << "Error Input Matrix" << endl;
return 0;
}
vector<int> empty_row_list;
vector<int> empty_col_list;
int unknown_num = get_empty_num(empty_row_list, empty_col_list);
runKernel(0, unknown_num, empty_row_list, empty_col_list);
return 0;
}
執行程式
我把全部的 code 放在 github 上。
最後看看結果。
$ g++ Sudoku.cpp
$ ./a.out
My words
這個題目不是很難,不過滿有樂趣又能練習遞迴,算是滿不錯的練習。為了快速驗證,我就沒有把它寫成 class,變數命名與寫法也比較隨便,但盡可能保持閱讀性。在 data structure 的使用上還有很多進步空間。
這不是很快的方法,不過也不算太慢。之後可以再來讀讀別人為了數獨而特別做的研究。
另外,我在 code 中寫死的困難數獨來自一位數學家設計的高難度題目。